Learning the fitness dynamics of pathogens from phylogenies – Nature
Sequence data
For each pathogen, we compiled a dataset to investigate the changes in the population composition. For SARS-CoV-2 and H3N2, we extracted the datasets from the publicly available NextStrain37 time-resolved phylogenies, accessed on 14 April 2023. These datasets are sub-samples from all publicly available sequences in GISAID, to represent the diversity as much as possible (we used the ‘all-time’ dataset for SARS-CoV-2 and the ‘12 y’ one for H3N2). In all, we have 3,129 whole-genome SARS-CoV-2 sequences sampled from 26 December 2019 to 3 April 2023, and 1,476 H3N2 HA sequences from 1 January 2005 to 3 April 2023 (Supplementary Tables 10 and 11). For B. pertussis, we used 1,248 sequences from 1953 to 2022, collected by the National Reference Center for Whooping Cough and Other Bordetella Infections in France (Supplementary Table 12). This dataset is composed of 1,023 previously published sequences3,38,39,40,41 and 225 newly sequenced isolates. The new isolates have been sequenced with the same methods as previously described3. This dataset is representative of the B. pertussis diversity in France as the National Reference Center receives isolates from 42 sentinel hospitals throughout France. For M. tuberculosis, we used 997 previously published sequences, isolated in 2008–2010 in Samara, Russia20. This dataset is also representative of M. tuberculosis sequence diversity at that location as isolates were prospectively collected from individual patients living in the region and representative of the entire population (Supplementary Table 13).
Multi-sequence alignment for each pathogen
We compiled alignments of all sequences. For SARS-CoV-2, we used the precomputed multi-sequence alignment provided by GISAID. For H3N2, we aligned all HA sequences using MAFFT42 (v.7.309) with default settings. We then manually checked that the alignment did not have any frameshift and had minimal gaps. For B. pertussis and M. tuberculosis, we worked from raw reads with a previously described protocol3. Reads were trimmed using Cutadapt43 (v.3.4) and quality was checked with FastQC44 (v0.11.9). Using BWA-MEM45 (v0.7.17), reads were mapped against the complete Tohama I reference genome (accession number in RefSeq: NC_002929) or the complete H37Rv reference genome (accession number in RefSeq: NC_000962.3). Using GATK46 (v.4.2.0.0), we kept variants that were present in at least 75% of reads, with a Phred quality score higher than 30, a minimum read depth of 5, a minimum mapping quality of 20 and a string odd ratio of less than 3. We masked all positions that were covered by less than five reads. Furthermore, we filtered out regions that are notoriously difficult to map and/or sequence, similarly to previous studies3,47. Namely, for B. pertussis we filtered out repeated regions (IS481, IS1002 and IS1663)35 and phage regions using PHASTER48; for M. tuberculosis, we filtered out the functional categories ‘PE/PPE’ and ‘insertion sequences and phages’47. For B. pertussis, we also checked for recombination in our alignment using Gubbins49 (v.3.3.0). As a result, we obtained an alignment of 4,701 SNPs for B. pertussis and 30,533 SNPs for M. tuberculosis.
Reconstruction of time-resolved phylogenies
For each pathogen, we obtained time-resolved phylogenies. For SARS-CoV-2 and H3N2, we used the NextStrain trees, accessed on 14 April 2023 (ref. 37). For B. pertussis and M. tuberculosis, we reconstructed the timed phylogenies specifically for this study using the SNP-based alignments. We first built maximum-likelihood trees using IQ-tree50 (v.2.1.0) using a GTR + F + G substitution model. To assess the branch support, we used the ultrafast bootstrap approximation provided in IQ-tree, performing 1,000 replicates for each dataset with the bnni option to reduce the risk of overestimating the branch support51.
For B. pertussis, the time tree was reconstructed using BEAST v.1.10.452, under a GTR substitution model18 accounting for the number of constant sites, a relaxed lognormal clock model53 and a skygrid population size model54. Three independent Markov chains were run for 150,000,000 generations each, with parameter values sampled every 10,000 generations. Runs were optimized using the GPU BEAGLE library55 (v.4.0.0). Chains were manually checked for convergence (effective sample size values > 200) using the Tracer software56 (v.1.7.2). We manually removed a 10% burn-in.
For M. tuberculosis, because all sequences were isolated in 2008–2010, we could not infer a clock rate, but instead, we used a previously estimated clock rate57 of 4.6 × 10−8 mutations per site per year. We used the software BactDating58 (v.1.1) to perform a Bayesian reconstruction of the time tree. We used a fixed mean substitution rate, a relaxed clock rate and a constant effective population size. We ran the chain for 10,000,000 iterations and checked for convergence (effective sample size values > 200).
Index definition
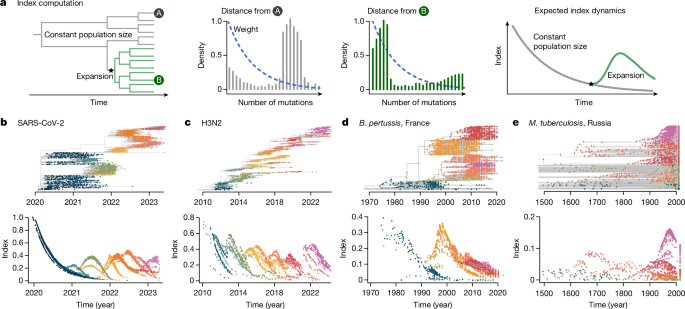
We developed an analytical approach that summarizes the changes in population composition in phylogenetic trees at every time point. Our approach builds on a genetic distance-based index, the timed haplotype density16, that measures the epidemic success of individual sequences in a dataset. This measure is based on the expectation that sequences sampled from an emerging, fitter lineage will be phylogenetically closer than the rest of the population at that time, as they will all share the same recent ancestor. We extend this method to track population changes in phylogenetic trees through time.
We define the index of each isolate i in its population at time t as:
$${\rm{Index}}(i)=\mathop{\sum }\limits_{d=0}^{\infty }{D}_{i}(d\,,t){b}^{d}$$
(1)
Where Di(d,t) the distance distribution—in number of mutations or evolutionary time (branch length)—from isolate i to the rest of the population (internal and terminal nodes) at time t (Fig. 1) and bd is the kernel setting the weight of each distance d. b is the bandwidth, b ∈[0, 1], which is a parameter to set, linked to the timescale. We compute this index on each node in a tree (internal and terminal).
The weight allows us to track lineage emergence dynamically, focusing on short distances between nodes (containing information about recent population dynamics) rather than long distances (containing information about past evolution). The kernel is governed by the bandwidth b, which is a parameter to set. As b is dimensionless, it is hard to set. Instead, we use the notion of timescale 50 to choose it: the time to the most recent common ancestor (TMRCA) was chosen such that pairs of isolates with shorter TMRCAs account for 50% of the kernel density16. This timescale is tailored to the specific pathogen studied and its choice will depend on the molecular signal, as well as the transmission rate. Here we used timescales ranging from 1.8 months (SARS-CoV-2, RNA virus) to 30 years (M. tuberculosis, a bacterium) (Supplementary Table 1).
Our approach provides a quantitative index value for each node (internal and terminal) in the tree, independently of any lineage classification providing an advantage over other methods that rely on lineage classification. This enables us to agnostically summarize the changes in population composition in phylogenetic trees at every time point.
Our definition is nearly the same as the one used in a previous study16, with two critical differences: instead of computing the index by summing on each isolate in the population we now sum over the pairwise distance distribution, and we consider the collection time of each sequence to only compute the distance from i to the rest of the population that is circulating at that time.
This index is similar to the local branching index10, which is defined as the total surrounding tree length exponentially discounted with increasing distance from isolate i. In our case, rather than considering the tree length, we compute the distance between nodes.
This index definition enables us to write an expectation of the index dynamics over time, as theoretical pairwise distance distributions can be approximated for different populations. In practice, to compute the index of each node in a phylogenetic tree, we sum over the distance to all nodes in the population, rather than the distance distribution (see ‘Index computation on time tree with sequences sampled through time’ section).
Linking the index dynamics to population history
The pairwise distance distribution Di(d,t) or more generally D(d,t), can be seen as the probability, \({P}_{c}(s=\frac{d}{\mu l},t)\), for any pair of sequences sampled at time t, to coalesce some time \(s=\frac{d}{\mu l}\) in the past, with μ being the rate at which the pathogen accumulates mutations per site and per unit of time and l the length of its genome.
$$D(d,t)={P}_{c}(s=\frac{d}{\mu l},t)$$
Therefore, at any time point, writing the probability of coalescing in the past enables us to compute the index in the population. We can update equation (1):
$${\rm{Index}}(t)={\int }_{0}^{\mu lt}{P}_{c}\left(\frac{u}{\mu l},t\right)\cdot {b}^{u}{\rm{d}}u$$
(2)
We note that at time t, the maximum number of mutations accumulated is equal to μlt. For simplicity, we assume a linear accumulation of mutations through time in all the analytical expressions, although one could consider that mutations accumulate randomly given a Poisson distribution with rate 1/(μlt).
This probability \({P}_{c}(s=\frac{d}{\mu l},t)\) is closely linked to the effective population size. In Supplementary Fig. 13, we show conceptually how, for different effective population sizes, the probability of coalescing changes, and how it affects the index dynamics. Formal derivations are presented in the Supplementary Information.
Index computation on time tree with sequences sampled through time
We use equation (1) to compute the index of each node (internal or terminal) in a timed phylogenetic tree. To do this, for each node i, we compute its distance to all the other nodes present in the tree at that time (see Supplementary Fig. 14 for notations). All the nodes that fall in the time interval [ti – twind; ti + twind] are considered to be circulating at the same time as i; with ti being the collection time of node i and twind the predefined time window width that is tailored to each pathogen. We also consider extant branches in the computation, as they are evidence of past circulation.
For computation efficiency, similarly to the previously published study16, we then compute:
$${\rm{Index}}(i)=\sum _{j\in {\rm{nodes}}}I({t}_{j} > {t}_{i}-{t}_{{\rm{wind}}}\,{\rm{and}}\,{t}_{j}
(3)
Where nodes indicates the set of all nodes in the tree, and I() is the indicator function.
This computation is efficient as it only requires the precomputation of the indicator function, the precomputation of the distance matrix and a matrix multiplication.
For the pathogens presented in our study we used the following parameters. SARS-CoV-2: a timescale of 0.15 years, and a window of time twind = 15 days. H3N2: a timescale of 0.4 years, and a window of time twind = 0.25 years. B. pertussis: a timescale of 2 years, and a window of time twind = 1 years. M. tuberculosis: a timescale of 30 years, and a window of time twind = 15 years.
We illustrate the impact of the timescale on the index dynamics in Extended Data Fig. 8 for the global SARS-CoV-2 tree.
To test the robustness of the index computation for the exact tree topology, we ran a sensitivity analysis on 3,000 trees sampled from the posterior of the BEAST run of B. pertussis. We chose B. pertussis for this analysis because it is the only pathogen for which we have a posterior distribution of trees. We repeatedly computed the index on each tree sampled from the posterior and computed the average index of each tip. Although there is uncertainty in the exact value of the index for each tip, we found that the index dynamics of each lineage remained very consistent across the posterior of trees (Supplementary Fig. 15).
Agnostic detection of lineages
We develop an approach that is able to find the set of lineages in the tree that best explains the index dynamics. To do this, we build an algorithm based on generalized additive models (GAM) that jointly uses the phylogenetic relationships between nodes in the tree and their index.
In this section, for modelling purposes, we define lineages as monophyletic clades formed by one internal node and all its descendants. Here, these lineages can overlap, meaning that some isolates can be included in multiple lineages. We assume the tree to be binary. For a rooted binary tree with n terminal nodes, there are n – 2 internal nodes that are not the root, and therefore n – 2 lineage possibilities—a substantial number. To keep the algorithm tractable, we limit the potential list of lineages to those starting with an internal node that has at least Noff offspring, where Noff is chosen. We note the set of internal nodes to test \(\Pi \). Furthermore, to increase the accuracy of the detection, we take into account only internal nodes that have predefined characteristics. For B. pertussis and M. tuberculosis, as we constructed the bootstrap support of each node (see above), we consider only internal nodes that have a bootstrap support of at least 50% to be the potential start of lineages. This threshold is low, but effectively removes nodes that are not well supported. For SARS-CoV-2 and H3N2, instead of bootstrap support, we consider a minimum number of mutations. We consider only internal nodes that have a least one mutation on the branch directly upstream from them.
The algorithm models the log index through time. We use a log transformation to avoid having to restrict to model to positive values and to make sure the model does not overfit the index peaks.
The log index of each lineage l is modelled using a cubic spline Sl(t, k) with a predefined number of knots k. This allows us to model the log index of each node i, sampled at time ti, given the lineage that it belongs to:
$$\log ({{\rm{I}}{\rm{n}}{\rm{d}}{\rm{e}}{\rm{x}}}_{i})={\beta }_{0}+{S}_{0}({t}_{i},k)+\mathop{\sum }\limits_{l=1}^{L}I(i\in l){S}_{l}({t}_{i},k)$$
Where β0 is the intercept, L is the total number of lineages, S0(t, k) and Sl(t, k) are penalized cubic regression splines with k knots59. One null spline S0(t, k) is estimated to model the initial population, together with one spline for each of the L lineages. If L = 0, then no Sl(t, k) is estimated. I() is the indicator function: I(i ∈ l) = 1 if i is a member of the lineage l, and 0 otherwise.
In brief, the algorithm runs as follows. We start with a null model M0 that fits the index dynamics with one spline S0(t, k) (that is, an unstructured population with one single index dynamic, L = 0). We store the deviance explained Dev0 by model M0. We then sequentially consider models with increasing complexity ML: we start by first trying models with one lineage, L = 1. We go through the list of internal nodes π that could be the start of a new lineage. When the deviance explained Dev1 by the best model M1 is higher than that of the previous null model Dev0 we keep the lineage (effectively the node from π) that best explains the dynamics. We then continue this procedure for increasing L. For each number L, we go through the list of internal nodes π that could be the start of a new lineage. When the deviance explained DevL by the model ML is higher than that of the previous model DevL–1, we keep the lineage (effectively the node from π) that best explains the dynamics.
The algorithm is implemented in R v.4.1.2, using the package mgcv v.1.8 (ref. 60) to implement the GAM models.
As for any clustering algorithm, choosing the best number of lineages that describe the index dynamics is a challenging question. We took the approach of the elbow plot. We plot the deviances DevL explained by each best model ML, as a function of the number of lineages L. This approach enables us to see how well all the models are performing, and to choose the number L of lineages at which the deviance explained does not increase substantially anymore (Extended Data Fig. 9). From this selected best number of lineages Lbest, we then compute the equivalent set of non-overlapping lineages presented in this paper (Figs. 1–5 and Extended Data Fig. 4). We make sure the minimum number of nodes per non-overlapping lineage is at least Nmin by merging the small lineages to their respective phylogenetically closest lineages.
In simulations, we demonstrate a clear elbow that precisely identifies the optimal number of discrete lineages in the dataset (Supplementary Fig. 16). However, not all pathogens in real-world datasets will give clear elbows. This may be due to insufficient sampling intensity and the presence of lineages with only very small differences in fitness. In practice, increasing the number of distinct lineages will progressively lead to the identification of lineages with increasingly reduced fitness differences, with increasing risks of falsely dividing lineages into subpopulations between which no true differences exist.
For the pathogens presented in our study we found: SARS-CoV-2, 14 lineages; H3N2, 20 lineages; B. pertussis, 8 lineages; and M. tuberculosis, 12 lineages.
To compare the automatic lineages found with phylowave to those previously identified, we compute a contingency matrix C. Let U be the partition of the isolates by phylowave and V the partition based on the literature. Each element Ci,j is the number of isolates in both clusters ui and vj. In Fig. 2, we plot the matrix as a heat map, normalized by column j. We computed the ARI to measure the agreement between partitions, accounting for random clustering21. A value of 1 corresponds to perfect agreement with previously identified lineages, whereas a value of 0 would be expected if clusters were assigned at random.
We illustrate the impact of the timescale on lineage detection in Extended Data Fig. 8 for the global SARS-CoV-2 tree.
Quantifying the fitness of each lineage
We developed a multinomial logistic model that takes into account the birth of lineages to fit the proportion of each lineage through time and quantify their fitness.
The proportion p•, t of sequences at time t from each lineage is computed as the number of nodes (internal and terminal) divided by the total number of nodes (internal and terminal) in the population at that time. This proportion p•, t is modelled by:
$${p}_{{\rm{\bullet }},t}={\rm{softmax}}(\log ({\alpha }_{{\rm{\bullet }}})+{\beta }_{{\rm{\bullet }}}t)$$
Where α• is the vector of the intercept, denoting the initial relative prevalence of each lineage in the population and β• the vector of the relative growth rates of each lineage. We assume that each lineage i has a constant relative growth rate βi in the population, that is, each lineage has a constant relative fitness through time. We compute all the relative growth rates with reference to the oldest lineage.
We use a Laplace prior for the growth rate coefficient (where ~ denotes ‘distributed as’)8:
$${\beta }_{{\rm{\bullet }}} \sim {\rm{Laplace}}(0,1)$$
We take into account lineage birth by only allowing only pi,t, the lineage i proportion in the population at time t, to be non-negative after the MRCA of the lineage. Formally, this is done by parameterizing α• as follows. We divide the lineages into two types, either ancestral or non-ancestral. An ancestral lineage is a lineage that is present at the beginning of the time series considered. The total number of ancestral lineages is noted G. For those lineages, we sample directly their starting proportions with prior:
$${\gamma }_{i} \sim {\rm{simplex}}(G);{\rm{if}}\,i\in {\rm{ancestors}}$$
A non-ancestral lineage is a lineage that appears after some time−for example the Omicron variant. For those lineages, we assume that their starting frequency, at the time of emergence, is a function of the proportion of their parents in the population at that time. Thus we write:
$${\alpha }_{i}={\gamma }_{i}{p}_{j,{t}_{{\rm{MRCA}}i}};{\rm{if}}\,i\notin {\rm{ancestors}}$$
Where j is the parent lineage of lineage i, \({p}_{j,{t}_{{\rm{MRCA}}i}}\) is the proportion of the parent lineage j at the time of emergence \({t}_{{\rm{MRCA}}i}\) of the offspring lineage i and γi is the share of the parent lineage that is becoming the new lineage. We sample γi with a strong prior because we expect that the starting proportion of new lineages should be small:
$${\gamma }_{i} \sim {\rm{beta}}(1,99);{\rm{if}}\,i\notin {\rm{ancestors}}$$
Finally, we update the parent j proportion as follows:
$${p}_{j,{t}_{{\rm{MRCA}}i}+\delta }=(1-{\gamma }_{i}){p}_{j,{t}_{{\rm{MRCA}}i}}$$
Although this parameterization is more complex than the previous efforts using a similar model8, it enables us to take into account that lineages appear through time, which makes the model more biologically relevant (for example, by not estimating the proportion of Omicron in the population in 2020). We chose to parameterize the starting proportions of the new lineages as a function of the proportion of their parents so that the model is biologically sound, that is, the starting proportion of a new lineage cannot be greater than the one of its parent, and the starting proportions are constrained by the proportion of the parents. The parameters make the model statistically easier to fit.
We use a multinomial likelihood to fit the count of sequences per lineage through time y•, t:
$${y}_{{\rm{\bullet }},t} \sim {\rm{multinomial}}\,(\sum _{i}{y}_{i,t},{p}_{{\rm{\bullet }},t})$$
We further computed the inferred real-time growth rate (that is, the fitness) ri(t) of each lineage i in the population (Fig. 3e–h), to control for the varying presence of all circulating lineages through time. Indeed, although our model estimates a constant fitness parameter for each lineage, their actual fitness through time depends on what other lineages are circulating at that time.
$${r}_{i}(t)={p}_{i,t}\sum _{\begin{array}{c}j\in {\rm{lineage}}s,\\ j\ne i\end{array}}{p}_{j,t}{(\beta }_{i}-{\beta }_{j})$$
These results are more useful than the usual presentation of the parameters, which by default display the relative fitness compared with the ancestral lineage, in this case 19A (the lineage that includes the first SARS-CoV-2 sequences isolated in Wuhan, China).
The model was implemented in Stan, using the cmdstanr package61. We ran this model on three independent chains with 1,000 iterations and 50% burn-in for each pathogen. We used 2.5% and 97.5% quantiles from the resulting posterior distributions for the 95% credible intervals of the parameters.
We fit the counts per lineage in windows of 1 month for SARS-CoV-2, 0.2 year for H3N2, 1 year for B. pertussis and 20 years for M. tuberculosis, with t counted in years for all pathogens.
Defining mutations of each lineage
We explored whether specific changes in the genomes were linked to lineage fitness by identifying lineage-defining mutations. We defined such mutations as follows: (i) mutations that are present in more than 80% of the nodes in that lineage; (ii) mutations that are not present in the set of defining mutations of the ancestral lineage.
For all pathogens, we reconstructed the mutations at each tree node using the ancestral state reconstruction implemented in the library ape. To maximize the correct assignment of nodes, we consider only nodes for which the probability of the state was >0.9. Mutations were then classified as synonymous, non-synonymous or extragenic. For M. tuberculosis and B. pertussis, we also classified each mutation by functional category35,36.
We computed the density of lineage-defining mutations along the SARS-CoV-2 full genome and H3N2 HA polyprotein with a kernel density estimate (Fig. 4e,f). We used a Gaussian kernel with a bandwidth of 50 base pairs for SARS-CoV-2, and a bandwidth of 2.5 amino acids for H3N2. For B. pertussis and M. tuberculosis, we plot for each mutation the maximum proportion of that mutation that is present in the set of groups considered.
To assess the functional relevance of the mutations identified for each pathogen (Supplementary Tables 6–9), we compared them with the literature.
For SARS-CoV-2, we matched the amino acid substitution we found with the ones that have been analysed previously8. The authors analysed 6.4 million genomes up to 20 January 2022 and estimated the fitness effect of 2,904 substitutions. Although our global dataset encompasses a longer period (up to 3 April 2023), 83% (n = 161) of the lineage-defining alterations had been analysed previously8. Our approach was able to recover all of the top 55 fittest alterations described previously8. Among the top 100 fittest alterations, our approach recovered 86% of them. The substitution missed by our method are mainly linked to small subclades of variants, and they seem to have spread in those clades only (for example, in subclades of Delta 21I: ORF1a(T3750I) and ORF1b(R188Q)). One substitution was missed because of a lack of certainty in the ancestral state reconstruction around the root of the Omicron sublineages: S(T376A). Of the alterations that were estimated to have no fitness increase, we found seven (among 2,331 analysed previously8). These alterations include S(D614G) and ORF1b(P314L), two alterations that are linked to an early lineage that eventually got fixed in the whole population. We also found ORF8(G8*) and S(G252V), which defined our lineage 1 (XBB1*), and ORF1a(L3829F), S(N460K) and ORF1b(M1156I), which defined our lineage 4 (22E/BQ.1). These substitutions were analysed by previously8 but were present only at a very small frequency in their dataset, as they are mainly linked to the emergence of recent variants, which emerged after their study.
For H3N2, we computed the proportion of positions that are lineage defining in each HA polyprotein subunit and the antigenic sites32,33. A position is lineage defining if it has at least one amino acid (AA) substitution that is lineage defining. The proportion is computed as follows:
$${\pi }_{L}=\frac{{\rm{Number}}\,{\rm{of}}\,{\rm{positions}}\,{\rm{that}}\,{\rm{are}}\,{\rm{lineage}}\,{\rm{defining}}\,{\rm{in}}\,L}{{\rm{Number}}\,{\rm{of}}\,{\rm{positions}}\,{\rm{that}}\,{\rm{are}}\,{\rm{mutated}}\,{\rm{in}}\,L}$$
Where L is the set of positions to be analysed (subunits or antigenic sites). We found that the Koel sites33 had the highest proportion of lineage-defining mutations, with 86% of positions (n = 6, out of 7) being recovered by phylowave. Specifically, the key positions 156, 159 and 193, defining multiple clades, were recovered. We also recovered positions that defined ancestral lineages, namely positions 145, 158 and 189. Furthermore, position 155 was not picked up by our method because it did not have any variability in our dataset. Indeed, this position was found to be linked to major antigenic changes in the 1960s and 1970s; this period does not overlap with our study period (2005–2023).
For the bacteria B. pertussis and M. tuberculosis we use a similar metric, by grouping mutations according to gene functional categories. We compute:
$${\pi }_{F}=\frac{{\rm{Number}}\,{\rm{of}}\,{\rm{AA}}\,{\rm{substitutions}}\,{\rm{that}}\,{\rm{are}}\,{\rm{lineage}}\,{\rm{defining}}\,{\rm{in}}\,F}{{\rm{Number}}\,{\rm{of}}\,{\rm{AA}}\,{\rm{substitutions}}\,{\rm{in}}\,F}$$
Where F is the gene functional category that we considered35,36. As a sensitivity analysis, we also replicated this computation on synonymous nucleotide changes, as we expect these mutations to be neutral, and therefore not linked to any particular functional category (Supplementary Fig. 17). We found that, indeed, there was no particular functional category that had significantly more lineage-defining synonymous mutations than others, for both bacteria.
To further check our findings visually, we plotted the lineage-defining mutations for each pathogen next to their phylogenetic trees (Supplementary Figs. 9–12). To make sure the figures were interpretable, we plotted only the mutations in the spike protein for SARS-CoV-2 (Supplementary Fig. 9), the HA1 subunit for H3N2 (Supplementary Fig. 10) and the mutations defining lineages 1 and 2 for M. tuberculosis (Supplementary Fig. 12). For B. pertussis, we plotted all mutations (amino acid substitutions and promoter mutations) (Supplementary Fig. 11).
Robustness to sampling strategies
To demonstrate the robustness to sampling biases over time, we conducted a sensitivity analysis using the global SARS-CoV-2 dataset. We selected two random sets of 150 sequences from the 3,129 sequences in our full dataset. We selected them either uniformly through time or in a temporally uneven manner. To do so, we divided the sequences in 15 time windows of equal length (79 days). For the uniform sampling, we included ten randomly selected sequences per time bin. For the biased sampling, we included the following number of sequences per bin (see inset on Fig. 5b): windows 1 and 2, 1 sequence per bin; windows 3–5, 2 sequences per bin; windows 6–9, 25 sequences per bin; windows 10–15, 7 sequences per bin.
After selecting the sequences, we pruned from the tree the ones that were not selected. We then performed the same analysis as described above. We also compared the groups found.
Analysis of time to detection
We explored how fast after emergence phylowave was able to detect lineages. To do this we truncated our full global SARS-CoV-2 dataset every two weeks. Overall, we obtained 81 datasets. Two examples of the index dynamics for data censored on 2021.26 and 2022.50 are presented in Extended Data Fig. 10. We then reran the detection algorithm on each dataset. To obtain the best set of lineages automatically for each dataset, we chose the set for which the log deviance explained did not increase by more than 0.01%.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Related
Yaslen Clemente Shows Off Leg Day Gains and Shares Her…
Yaslen Clemente isn't just an influencer—she's a fitness powerhouse. The social media star is known for her intense workouts, and she recently sha
Samantha Espineira Stuns in Blue Swimsuit and Shares Her 5…
Samantha Espineira knows how to turn heads, both on and off the runway. The successful model and Instagram influencer regularly shares breathtaking
The Best Fitness Trackers To Help You Reach Any Health…
Best Health Tracker: Oura Ring 3Why We Love It: I’ve tried many, many fitness trackers—but I tend not to stick with one watch or band for very long. I’ve
#CycleSyncing debunked: Popular TikTok trend not backed by science
A new study has debunked a popular TikTok wellness trend called cycle syncing, which claims that tailoring a workout routine to match the hormonal changes that












