Genomic and fitness consequences of a near-extinction event in the northern elephant seal - Nature Ecology & Evolution

Genomic and fitness consequences of a near-extinction event in the northern elephant seal – Nature Ecology & Evolution

Posted by Admin September 27, 2024 Fitness

Northern elephant seals

Tissue samples were obtained from juvenile elephant seals that died from various causes between 2006 and 2012 at The Marine Mammal Center (Sausalito, CA, USA) following stranding along the California coast from San Luis Obispo to Humboldt County. At admittance, the animals were weighed (kg) and their blubber thickness (cm) was measured over the sternum. Within 24 h of death, each animal was subjected to a standardized postmortem examination. Helminth infections were identified by examining the respiratory tract, heart and great blood vessels and gastrointestinal tract. Representative samples of internal organs were fixed in 10% neutral buffered formalin, embedded in paraffin, sectioned at 5 µm and stained with haematoxylin and eosin for light microscopy to examine the tissues histologically. As described by Colegrove et al.⁷² the cause of death was defined as the disease or condition that was the most likely cause of the animal’s death based on all of the available information. Each individual was assigned to one of the following categories:

(1)

Helminth infection (n = 62): clinical manifestations of Otostrongylus circumlitus infection, including neutrophilia, disseminated intravascular coagulation and fatal inflammatory reaction.
(2)

Bacterial infection (n = 28): primary infection with a specific microbial organism (for example, Leptospira or Salmonella species) or generalized non-specific bacterial infection following trauma or malnutrition.
(3)

Protozoan infection (n = 4): infection with a protozoal parasite (for example, Toxoplasma gondii, Sarcocystis species or Eimeria species).
(4)

Trauma (n = 19): wounds with no complicating generalized infections, including boat strikes, bite wounds, lacerations and musculoskeletal injuries.
(5)

Malnutrition (n = 88): poor body condition with no other obvious infections or lesions.
(6)

Congenital defects (n = 18): the presence of a major congenital defect that contributed to poor health, either causing death or resulting in euthanasia due to a poor veterinary prognosis.

Finally, a ~5 mm³ skin sample was collected from the foreflipper of each animal with a scalpel and stored in 95% ethanol at −20 °C for subsequent analysis. All animal care and sampling procedures were authorized by the National Marine Fisheries Service (MMPA permit number 18786) and approved by The Marine Mammal Center’s internal animal care and use committee.

Southern elephant seals

Tissue samples were obtained from 20 southern elephant seals (one adult female, three adult males and 16 pups) from a breeding colony at Half Moon Beach, Cape Shirreff in the South Shetland Islands (62° 28′ 37.4′′ S, 60° 46′ 45.0′′ W) between 2008 and 2015 (see Nichols et al.⁷³ for details). Adults were sampled from the flanks using a 2 mm sterile disposable Miltex biopsy punch (Thermo Fisher Scientific). Pup skin samples were collected from a rear flipper using a tag hole punch or a 2 mm sterile disposable Miltex biopsy punch. The samples were immediately transferred to 95% ethanol and stored at −20 °C until subsequent analysis. All sampling was conducted in accordance with Marine Mammal Protection Act permit numbers 16472-01 and 774-1847-04, granted by the Office of Protected Resources, National Marine Fisheries Service (Antarctic Conservation Act permit numbers 2012-005 and 2008-008). The protocols used in this study were also reviewed and approved by the US National Marine Fisheries Service Southwest and Pacific Islands regions’ Institutional Animal Use and Care Committee (approval documents SWPI2011-02 and SWPI2014-03).

Microsatellite genotyping

Total genomic DNA was extracted from the northern elephant seal samples using a modified phenol–chloroform protocol and genotyped at 22 polymorphic microsatellite loci (Supplementary Table 1). The loci were PCR amplified in four separate multiplexed reactions using a Type-it kit (Qiagen). The following PCR profile was used: initial denaturation of 5 min at 94 °C; 28 cycles of 30 s at 94 °C, 90 s at the annealing temperature (T_a °C) specified for each multiplex reaction in Supplementary Table 1, and 30 s at 72 °C, followed by a final extension of 30 min at 60 °C. Fluorescently labelled PCR products were then resolved by electrophoresis on an ABI 3730xl capillary sequencer and allele sizes were scored using GeneMarker version 1.95. To ensure high genotype quality, all traces were manually inspected and any incorrect calls were adjusted accordingly. We also quantified the genotyping error rate for the resulting dataset by independently repeat genotyping 85 samples between one and five times each. This was very low at 0.0016 per locus or 0.0013 per allele. Finally, deviations from Hardy–Weinberg equilibrium were calculated for each microsatellite locus using chi-squared tests and exact tests based on 1,000 Monte Carlo permutations of the dataset⁷⁴ implemented in the R package pegas 1.0-1 (ref. ⁷⁵). The resulting P values were corrected for the false discovery rate using the R package qvalue⁷⁶. The R package adegenet⁷⁷ was also used to calculate the observed and expected heterozygosity of each locus.

RAD sequencing

A representative subset of 96 northern elephant seals (33 animals with helminth infection, 19 with bacterial infection, two with protozoan infection, 11 with trauma, 22 with malnutrition and nine with congenital defects) was chosen for RAD sequencing. The libraries were prepared using a modified protocol from Etter et al.⁷⁸ with minor modifications as described by Hoffman et al.³⁷. Briefly, 400 ng genomic DNA from each individual was separately digested with SbfI followed by the ligation of P1 adaptors with a unique 6 bp barcode for each individual in a RAD sequencing library, allowing the pooling of 16 individuals per library. Libraries were sheared with a Covaris S220 and agarose gel size selected to 300–700 bp. Following 15–17 cycles of PCR amplification, the libraries were further pooled using eight different i5 indices before 250 bp paired-end sequencing on two Illumina HiSeq 1500 lanes. This resulted in a total of 315,558,810 paired-end 250 bp Illumina sequence reads.

The quality of the raw sequences was checked using FastQC⁷⁹ and low-quality reads were trimmed using the fastx_trimmer module within the FASTX-Toolkit (http://hannonlab.cshl.edu/fastx_toolkit). Subsequently, the reads were demultiplexed using the process_radtags module within the Stacks pipeline⁸⁰ and any reads containing uncalled bases or reads with an average phred scaled quality score below ten within sliding windows comprising 15% of the length of the read were discarded. We then used the bwa-mem algorithm in BWA⁸¹ with default parameters to align the demultiplexed reads to the M. angustirostris reference genome, available via the National Center for Biotechnology Information (NCBI; RefSeq identification code GCF_021288785.2). The resulting SAM files were converted to BAM format and sorted by coordinate using SAMtools⁸². Next, Picard tools (https://broadinstitute.github.io/picard) was used to add read groups to individual BAM files and to mark and remove PCR duplicates. Finally, variant discovery and calling was implemented using the HaplotypeCaller module within GATK⁸³ and the resulting 321,124 raw genotypes were filtered using VCFtools⁸⁴ and PLINK⁸⁵ to retain only high-quality biallelic SNPs. Specific filtering steps included: (1) retaining only individual genotypes with a depth of coverage and genotype quality of greater than five; (2) removing loci that could not be called in more than 50% of individuals; (3) removing loci whose coverage exceeded twice the mean coverage of the dataset (19.06×); (4) removing loci that deviated significantly from Hardy–Weinberg equilibrium based on a P value threshold of 0.01 after having implemented mid-P adjustment, as described by Graffelman and Moreno⁸⁶; (5) removing loci with a minor allele frequency below 0.01; and (6) removing samples with more than 50% of missing data. The final quality-filtered dataset comprised 74 individuals genotyped at 15,051 SNPs.

Population structure

To test for the presence of population genetic structure, we subjected both the microsatellite and RAD sequencing datasets to PCA using the R package adegenet^77,87. Specifically, we applied the function dudi.pca to the microsatellite data and the glPca function to the SNP dataset. The glPca function is specifically designed to efficiently compute PCA on large SNP datasets.

Identity disequilibrium

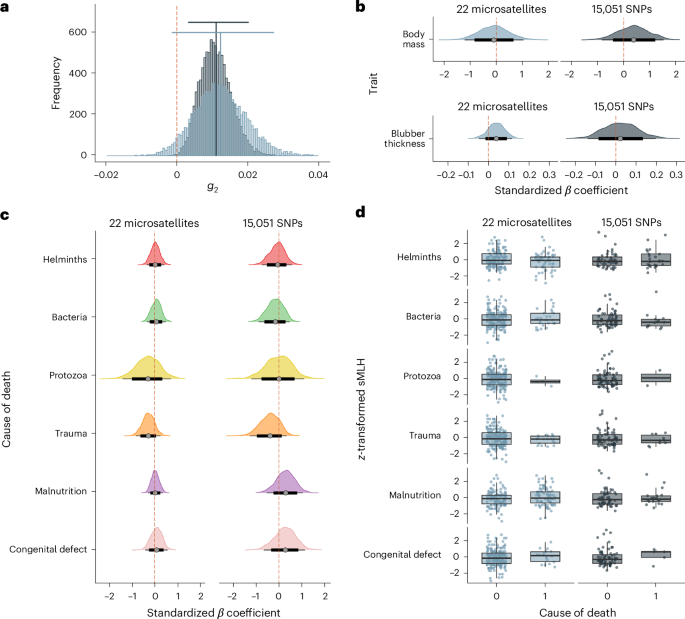
To quantify the variance in inbreeding, we calculated the two-locus heterozygosity disequilibrium (g₂)³⁵ for the microsatellite and RAD sequencing datasets using the R package inbreedR⁸⁸ version 0.3.3. The 95% CIs of g₂ were determined based on 100 permutations of the dataset and bootstrapping 10,000 times over individuals. InbreedR was also used to quantify individual sMLH for both the microsatellite and RAD sequencing datasets.

Inbreeding depression

To test for inbreeding depression for body mass and blubber thickness, we constructed Bayesian linear mixed models using the R package brms⁸⁹ version 2.19.0. The predictor variable was z-transformed sMLH, and sex and the month and year of admittance were included as random effects, as follows:

$${\text{mass}}_{{ij}}={{{\beta}}}_{0}+{{{\beta }}}_{1}\times {\text{sMLH}}_{{ij}}+{b}_{i}+{u}_{j}+{v}_{k}$$

$${\text{blubber}}_{{ij}}={{{\beta }}}_{0}+{{{\beta }}}_{1}\times {\text{sMLH}}_{{ij}}+{b}_{i}+{u}_{j}+{v}_{k}$$

where:

${\text{mass}}_{{ij}}$ represents the observed value of the response variable mass for observation i within the levels of the grouping variables sex (i), month (j) and year (k);

${\text{blubber}}_{{ij}}$ represents the observed value of the response variable blubber thickness for observation i within the levels of the grouping variables sex (i), month (j) and year (k);

${\beta }_{0}$ and ${\beta }_{1}$ are the fixed-effects coefficients for the intercept and the predictor variable sMLH, respectively;

${b}_{i}$ represents the random intercept for each level of the grouping variable sex;

${u}_{j}$ represents the random intercept for each level of the grouping variable month; and

${v}_{k}$ represents the random intercept for each level of the grouping variable year.

To investigate whether inbreeding is related to the most likely cause of death, we constructed Bayesian GLMMs separately for each of the six categories (helminth infection, bacterial infection, protozoan infection, trauma, malnutrition and congenital defects). For this, we used binomial classifications (that is, animals whose most likely cause of death was helminth infection were classified as 1 for helminth infection and 0 for all of the other categories). Again, z-transformed sMLH was fitted as the predictor variable, and sex and the month and year of admittance were included as random effects:

$$\log \left[\frac{{p}_{{ij}}}{1-{p}_{{ij}}}\right]={\beta }_{0}+{\beta }_{1}\times {\text{sMLH}}_{{ij}}+{b}_{i}+{u}_{j}+{v}_{k}$$

where:

${p}_{{ij}}$ represents the probability that the binary response variable category (for example, helminth infection and so on) is equal to 1 (died of the respective disease or condition) for observation i within the levels of the grouping variables sex (indexed by i), month (indexed by j) and year (indexed by k).

We also ran a similar analysis, but instead of using the binary classification of the most likely cause of death, we constructed a single multinomial GLMM with a categorical response variable, where each category was compared with the reference category trauma:

$${{\rm{logit}}}\left[P\left({Y}_{{ij}}\le m\right)\right]={{\rm{\alpha }}}_{m}-{{\beta }}\times {{\rm{sMLH}}}_{{ij}}+{b}_{i}+{u}_{j}+{v}_{k}\,{\rm{for}}\,{m}=1,2,\ldots k-1$$

where:

${{\rm{logit}}}\left[P\left({Y}_{{ij}}\le m\right)\right]$ is the log-odds of ${Y}_{{ij}}$ being less than or equal to category m; and

${\alpha }_{m}$ is the threshold parameter associated with category m.

Lastly, to investigate whether inbreeding differed between animals that died from trauma and those that died from other causes, we constructed Bayesian GLMMs using a binomial classification where animals whose most likely cause of death was trauma were classified as 0 and all other categories apart from trauma (that is, helminth infection, bacterial infection, protozoan infection, malnutrition and congenital defects) were classified as 1. Again, z-transformed sMLH was fitted as the predictor variable, and sex and the month and year of admittance were included as random effects:

$$\log \left[\frac{{p}_{{ij}}}{1-{p}_{{ij}}}\right]={\beta }_{0}+{\beta }_{1}\times {\text{sMLH}}_{{ij}}+{b}_{i}+{u}_{j}+{v}_{k}$$

where:

${p}_{{ij}}$ is the probability that the binary response variable category is equal to 1 (did not die from trauma) for observation i within the levels of the grouping variables sex (indexed by i), month (indexed by j) and year (indexed by k).

All of the above models were implemented separately for the microsatellite and RAD sequencing datasets. Three independent Markov chains were run for 100,000 iterations, using a thinning interval of 100 and burn-in of 50,000 iterations. We used generic weakly informative priors for the population-level effects. Model diagnostics, including autocorrelation and R hat statistics, and effective sampling sizes were generated using the R package bayesplot version 1.10.0 (ref. ⁹⁰). All statistical analyses were implemented in R version 3.6.3 (ref. ⁹¹) with Rstudio version 1.3.1093 using the tidyverse R package⁹² version 1.3.1.

Demographic reconstruction

To reconstruct past changes in the effective population size of the northern elephant seal, we performed demographic inference based on the folded SFS derived from genotype likelihoods. Specifically, the program ANGSD⁹³ was used to calculate genotype likelihoods based on the BAM files obtained after mapping the sequencing reads to the reference genome and filtering to remove alignments to the sex chromosome. This was implemented while retaining only uniquely mapped reads with a minimum mapping quality of 20, for which we also calculated base alignment quality scores to reduce errors deriving from misalignments around indels⁹⁴. Moreover, we retained only sites present in all individuals that had a minimum and maximum depth of coverage of 288 and 1,600, respectively, across all individuals. The resulting genotype likelihoods were then used as input to the ANGSD module realSFS to estimate the empirical folded SFS.

Demographic inference was implemented using the coalescent simulator fastsimcoal2 (ref. ⁹⁵), which we used to compare three alternative demographic models (Extended Data Fig. 3). The first model included a recent bottleneck spanning the peak of commercial exploitation of the northern elephant seal in the nineteenth century. The bottleneck was fixed between 23 and 17 generations ago, corresponding to the known period of intensive harvesting (1810–1860)^24,25 assuming a generation time of 8.7 years⁹⁶. The second model accounted for the fact that northern elephant seals continued to be hunted at a lower level until the end of the nineteenth century^25,26. Accordingly, the bottleneck was fixed between 23 and 13 generations ago. The third model did not include a recent bottleneck and therefore represented a null model. All of the models included a period of post-glacial population expansion, whose end, measured in generation ago, was inferred from the model. We denoted this time point (i.e. the end of the post-glacial expansion) as T_se. We included post-glacial expansion in our models because a previous comparative study of pinnipeds based on microsatellites found greater support in northern elephant seals for a demographic model that included a recent bottleneck and post-glacial expansion than a model that included only a recent bottleneck⁶⁷.

In all of these models, the defined initial search range for the current effective population size (N_ePOSTBOT) was log uniformly distributed between 5,000 and 40,000. For the bottleneck models, the defined initial search range for the effective population size before sealing (N_ePREBOT) was log uniformly distributed between 5,000 and 40,000, whereas the defined initial search range for the effective population size during the bottleneck (N_eBOT) was uniformly distributed between one and 50. Then, we defined the initial search range for the effective population size after the LGM (N_eLGM) between 50 and 4,000 and set the LGM to 2,100 generations ago, corresponding to approximately 19,000 years ago⁹⁷. Finally, the initial search range for T_se was uniformly distributed between 100 and 1,000 generations ago. Note that the composite maximum likelihood approach implemented in fastsimcoal2 uses these search ranges solely as starting values and the resulting parameter estimates can therefore exceed the upper limits⁵⁵.

A total of 100 replicate runs were performed for each model, including 100 estimation loops with 100,000 coalescent simulations. We did not include singletons in the simulations, as these can be biased when the sequence coverage is low⁹⁸. Out of the 100 replicates for each model, the run with the highest maximum likelihood was retained. The best model was then determined based on the delta likelihood values (the difference between the estimated and observed likelihoods) and Akaike’s information criterion values. Finally, we investigated the uncertainty of our parameter estimates by bootstrapping the data 100 times over individuals with replacement and using ANGSD to generate corresponding SFSs. For each of these 100 SFSs, the parameters were then re-estimated based on 100 replicate runs, each including 100 estimation loops with 100,000 coalescent simulations. For each SFS, the run with the top maximum likelihood was retained and used for the bootstrap distribution. For each parameter, 95% CIs were then calculated based on the resulting 100 bootstrap estimates.

Finally, to explore the sensitivity of our results to different types of input data, we repeated the demographic inference described above using SFSs obtained from WGS data from 20 northern elephant seals (for details, see below). The genotypes were filtered to include only autosomes using VCFtools and the corresponding SFSs were obtained using easySFS (https://github.com/isaacovercast/easySFS). Demographic inference was then implemented as described above for the RAD sequencing data, using the same models and priors.

Wright–Fisher simulations

To investigate how the inferred bottleneck may have impacted the genetic load of the northern elephant seal, we implemented forward genetic simulations with the software SLiM3 (ref. ⁵⁸). Specifically, we ran 100 Wright–Fisher simulations where we modelled the demographic history of the species since the LGM using point N_e estimates derived from the best-supported demographic model based on the RAD sequencing data (see ‘Results’). Starting from one generation before the bottleneck, we then quantified the following components of the genetic load of each simulated generation according to Bertorelle et al.¹²:

(1)

Total load. This represents the total number of lethal equivalents present in the population. It is quantified as the sum of the effect sizes of all deleterious mutations multiplied by their allele frequencies. It is thus independent of genotype frequencies and incorporates both the component of the genetic load that is expressed (that is, the realized load; see below) and the component of the genetic load that is not expressed (that is, the inbreeding load; see below).
(2)

Realized load. This is the fraction of the total load that is expressed and which therefore actively decreases the fitness of the population. It is determined by homozygous deleterious mutations and heterozygous deleterious mutations that are not fully recessive, whose effects are scaled by their dominance coefficients. Therefore, the realized load is quantified as the sum of the effect sizes of all homozygous mutations multiplied by their genotype frequencies plus the sum of the effect sizes of heterozygous mutations multiplied by their genotype frequencies and respective dominance coefficients.
(3)

Inbreeding load. This is the fraction of the total load that is masked in the heterozygous state. It is quantified by subtracting the realized load from the total load. This is the load component that determines inbreeding depression, as inbreeding unmasks the effects of deleterious mutations that are shielded from selection in the heterozygote state.
(4)

Drift load. This is the subset of the realized load that is represented exclusively by deleterious mutations that have drifted to fixation. We calculated this as the sum of the effect sizes of all fixed deleterious mutations.

We simulated the entire northern elephant seal genome, comprising all 17 autosomes, and allowed only deleterious mutations to arise. A burn-in of 10 × N_e generations was implemented to establish an equilibrium level of genetic diversity through mutation–selection balance. We modelled the evolution of deleterious mutations based on the available information to date²². First, these mutations were modelled to appear at a rate greater than one (U ≅ 1.2), which is in accordance with empirical estimates from fruit flies⁹⁹ and humans¹⁰⁰. Second, the distribution of fitness effects of the deleterious mutations was modelled as strongly bimodal, with the majority of mutations having small to moderate effects while a minority were lethal or semi-lethal¹⁰¹. This was achieved by sampling |s| from a gamma distribution with the mean and shape parameter equal to −0.04 and 0.2, respectively. Third, dominance coefficients (h) were modelled so that nearly neutral mutations were slightly recessive and highly deleterious mutations were nearly fully recessive, in accordance with empirical observations in fruit flies¹⁰² and yeast¹⁰³. For this we assumed the relationship between h and |s| provided by Deng and Lynch¹⁰⁴. Finally, deleterious mutations were allowed to appear throughout the genome—an assumption we believe to be realistic as deleterious mutations are known to arise not only within exons but also in regulatory elements and ultra-conserved genomic regions²¹. Nevertheless, for comparison, we also re-ran the simulations while allowing deleterious mutations to arise only within exons.

Finally, we incorporated the uncertainty associated with our demographic estimates by re-running the forward genetic simulations described above using the N_e estimates obtained from the bootstrapped SFSs, rather than a single point estimate from the best-supported demographic model, as input values. For comparison, we also ran an additional set of 100 simulations using the point N_e estimates obtained from the best-supported demographic model based on the WGS data.

Whole-genome analyses

Laboratory methods

A representative selection of 20 northern elephant seals that passed stringent quality control (ten animals with helminth infection, three with bacterial infection, four with trauma and three with malnutrition) were subjected to WGS, together with 20 southern elephant seals. The DNA samples were measured photometrically using a NanoDrop One instrument (Thermo Fisher Scientific) to determine purity. DNA quality was determined by capillary electrophoresis using the Fragment Analyzer and DNF-464 HS Large Fragment 50 kb Kit (Agilent Technologies) and the final specific DNA concentration was determined using the fluorometric Qubit dsDNA BR assay (Thermo Fisher Scientific). Library preparation was performed according to the manufacturer’s protocol using the Illumina DNA PCR-Free Prep, Tagmentation (Illumina) with a total input of >300 ng per sample. Libraries were normalized to 2 nM, pooled and sequenced on a NovaSeq 6000 (Illumina) with a read setup of 2 × 151 bp.

Variant calling

The genotyping of the WGS data from the northern and southern elephant seals was based on the GATK best practice recommendations¹⁰⁵. The reference genome for the whole-genome analysis was the M. angustirostris genome, available via NCBI (RefSeq identification code GCF_021288785.2). Before genotyping, scaffolds smaller than 1 kb were removed. A subset of the analysis was also repeated with the M. leonina genome (RefSeq identification code GCF_011800145.1) as a reference. The genotyping included the conversion of the raw sequencing data into ubam format for the assignment of read groups and the marking of Illumina adaptor sequences. Subsequently, the data were mapped to the reference genome using BWA and duplicated reads were marked. Using the GATK tool HaplotypeCaller¹⁰⁶, genotype likelihoods were obtained for each sample and the final genotypes were called jointly on all samples using the GATK tool GenomicsDBImport. A threshold-based hard filtering of the raw genotypes was applied based on the metrics QD (17.5), MQ (3.0), MQRankSum (0.5) and ReadPosRankSum (2.25). These thresholds were determined visually following the Broad Institute’s recommendations on the hard filtering of germline short variants (https://gatk.broadinstitute.org/hc/en-us/articles/360035890471). Subsequent to the genotyping with GATK, missing genotypes were reformatted from the Broad Institute’s notation (GT:0/0,DP:0) to the standard vcf representation (GT:./.) using the BCFtools plugin +setGT¹⁰⁷ to prevent missing data from being erroneously interpreted as homozygote genotypes in the downstream analysis.

Quality control

The quality of the resequencing data was assessed with FastQC and interspecific contamination was ruled out with FastQScreen¹⁰⁸. Mapping success was monitored with bamcov (https://github.com/fbreitwieser/bamcov) and BamTools¹⁰⁹. To further rule out intraspecific contamination, a combination of VCFtools, GATK VariantsToTable and custom R scripts were used to check for allelic imbalance within the called SNPs for each individual. MultiQC¹¹⁰ was used to monitor the quality control procedure and bundle individual reports.

Genetic diversity

To compare SNP densities between northern and southern elephant seals, VCFtools was used to create two subsets of genotypes, comprising only samples of one of the two species, respectively. These subsets were then filtered for a minor allele count of >1 to remove any invariant SNPs. Then, for both subsets, VCFtools was used to estimate SNP densities within non-overlapping 100 kb windows along the genome. For the estimation of nucleotide diversity (π), the genotyping step was repeated from the GenotypeGVCFs step onward, now including the flag –include-non-variant-sites true to also include invariant sites (the subsequent steps were unchanged). Based on this dataset, the Python scripts within the GitHub repository genomics_general (https://github.com/simonhmartin/genomics_general) were used to compute π within 100 kb sliding windows with 25 kb increments. Additionally, individual heterozygosity was summarized within 1 Mb sliding widows with 250 kb increments using a combination of VCFtools and custom R scripts.

ROH calling

ROHs were called in both elephant seal species using BCFtools¹¹¹ and PLINK⁸⁵. The BCFtools approach was implemented using the default parameters for the species subsets of the genotypes separately. For the PLINK analysis, a broad parameter space was explored by varying the input parameters over all possible combinations of –homozyg-window-snp 50, –homozyg-snp 100, –homozyg-kb [1000, 10], –homozyg-gap [1000, 50], –homozyg-density 50, –homozyg-window-missing [5, 20], –homozyg-het [1000, 0, 2] and –homozyg-window-het [1, 3] (a total of 48 parameter combinations). To evaluate the accuracy of the ROH calling, the resulting ROHs were then compared with patterns of genome-wide heterozygosity at the individual level using a combination of VCFtools and custom R scripts. Based on the close resemblance between the ROHs called by BCFtools and regions of low heterozygosity, the BCFtools results were favoured over the PLINK results for further analysis. A conservative minimum ROH length threshold of 1 Mb was then applied to facilitate comparisons with previous studies^112,113.

Genomic mutation loads

To identify functionally relevant SNPs in the genomes of the northern and southern elephant seals, genotypes within coding sequences were annotated using SnpEff⁶⁸. For this analysis, we obtained the northern elephant seal genome annotation from NCBI (GCF_021288785.2_ASM2128878v3_genomic.gtf.gz) and extracted protein and coding sequences using the tool gff3_to_fasta from the GFF3toolkit (https://github.com/NAL-i5K/GFF3toolkit). A custom SnpEff database was then created using the SnpEff build command and the VCF file with the genotypes was annotated using the ann command with the flags -no-downstream, -no-intergenic, -no-intron, -no-upstream and -no-utr. Variants categorized as high-impact or loss-of-function variants were classified as putatively harmful mutations and included in the load scoring.

Next, we assigned ancestral alleles using a cactus¹¹⁴ alignment of the two elephant seal genomes and the Weddell seal genome (RefSeq identification code GCF_000349705.1). Pairwise nucleotide differences between the M. angustirostris genome and the inferred shared ancestor of the three seal species were exported from the alignment using halSnps¹¹⁴. The VCF file containing the genotypes was then further annotated with the inferred ancestral alleles using the vcf-annotate tool from VCFtools. Lastly, Jvarkit¹¹⁵ was used in combination with a custom Java script to recode the genotypes based on their ancestral state (with 0 being ancestral and 1 being derived).

Finally, genomic mutation load estimates were obtained for all individuals using SnpSift¹¹⁶. For the inbreeding load, variants with putatively harmful mutations for the derived allele in the heterozygous state were tallied; for the segregating drift load, variants with putatively harmful mutations that were homozygous for the derived allele were scored. To estimate the magnitude of the drift load of each species, the genotypes were subsetted to include only SNPs that were invariant within each respective species. Then, for each subset, the number of SNPs that were fixed for the derived allele and that were classified as putatively harmful mutations was tallied using a combination of custom R scripts and SnpSift.

Non-Wright–Fisher simulations

To investigate how close the northern elephant seal came to extinction and explore the probable impact of deleterious mutations on the recovery of the population, we implemented non-Wright–Fisher simulations in SLiM3. We modelled overlapping generations and implemented age-dependent mortality so that most females produced fewer than nine pups in total¹¹⁷ and successful males died within a couple of years of first reproduction¹¹⁸. Mortality probabilities for the first four years of life were set to 0.632, 0.294, 0.253 and 0.160, respectively, according to Le Boeuf et al.¹¹⁹. Reproduction was implemented according to a harem-style system in which a small proportion of males reproduce with numerous females, each of which produce a single offspring per year. Le Boeuf¹¹⁸ reported that the majority of copulations at Año Nuevo in California were undertaken by the five most active males, which accounted for less than 5% of the male population. We therefore set the proportion of reproducing males to 5% to account for the additional contributions of small numbers of opportunistic males with very low reproductive success. The age at first reproduction was set to 4 years for females, as this is the most common age at primiparity in female northern elephant seals¹¹⁷, and 6 years for males¹¹⁸. The effect of deleterious mutations was assumed to be constant through all age classes and for each sex and was implemented entirely through survival, meaning that the genetic load purely affected the probability of an individual surviving to the next simulation cycle.

Census population sizes were determined by setting the carrying capacity (K) through time to appropriate values in the simulations. Given that the contemporary northern elephant seal population consists of around 225,000 individuals³⁰, we set the post-bottleneck K to 350,000 to allow our simulated population to reach a contemporary N_c similar or greater than the empirical value. The N_c estimate of Lowry et al.³⁰ was also used to derive the census-to-effective population size ratio, which we then used to convert our historical N_e estimates from the demographic model into N_c values, and set the corresponding carrying capacities accordingly. N_c at the start of the simulation (that is, preceding post-glacial expansion) was set to 2,670 (10 × N_eLGM) assuming an N_e-to-N_c ratio of 0.1. This was implemented as a time-effective solution for reaching an equilibrium level of genetic diversity during a burn-in of 26,700 simulation cycles, during which we implemented random mating. To investigate the effect of bottleneck strength on extinction risk and post-bottleneck population recovery, we set the bottleneck K to 50, 100, 250, 500 and 1,000 and ran 100 simulations for each value. These values were chosen to allow comparisons to be made between strongly and weakly bottlenecked populations. Then, separately for each bottleneck scenario, we quantified the extinction probability as the proportion of simulations in which the northern elephant seal population went extinct. In addition, we extracted N_c and fitness values one generation before the bottleneck, as well as for each generation after the bottleneck (that is, every nine years, assuming a northern elephant seal generation time of 8.7 years). Simulated post-bottleneck demographic recovery trajectories were then compared with empirical values obtained from Bartholomew and Hubbs²⁷, Le Boeuf and Bonnell²⁸, Stewart et al.²⁹ and Lowry et al.³⁰.

Finally, we ran a series of neutral models to test whether any demographic patterns emerging from the non-Wright–Fisher models described above could be attributed to the stochasticity associated with the population decrease imposed by the bottleneck, rather than to fitness effects deriving from deleterious mutations. To do so, we re-ran all of the non-Wright–Fisher simulations while suppressing the onset of deleterious mutations and keeping everything else unchanged. Five simulations were run for each value of K.